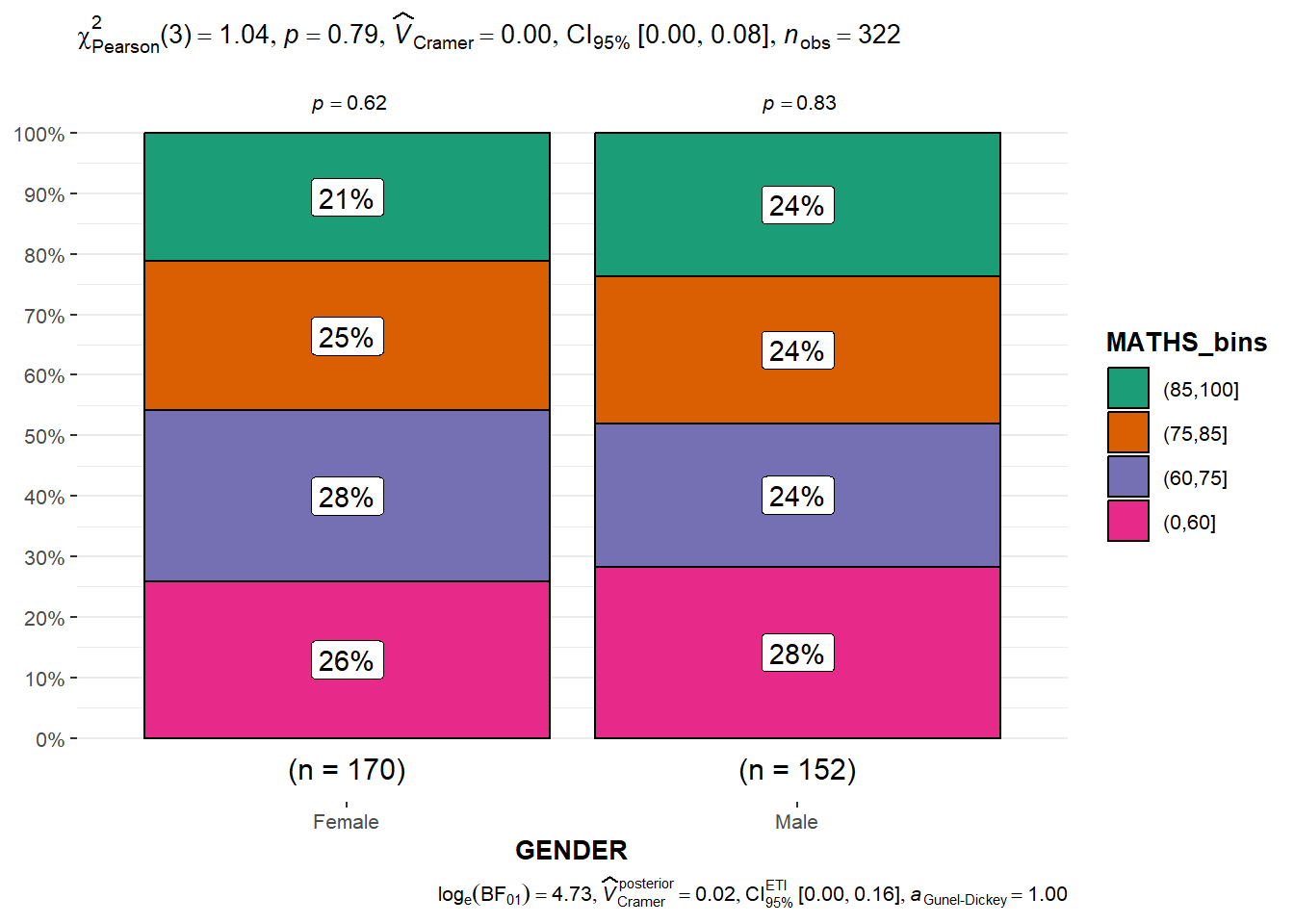pacman::p_load(ggstatsplot, tidyverse)Hands-on_Ex04_b
Learning Outcome
ggstatsplot package to create visual graphics with rich statistical information
performance package to visualise model diagnostics
parameters package to visualise model parameters
Getting Started
Installing and launching R packages
In this exercise, ggstatsplot and tidyverse will be used.
Importing data
exam <- read_csv("Exam_data.csv")One-sample test: gghistostats() method
In the code chunk below, gghistostats() is used to to build an visual of one-sample test on English scores.
set.seed(1234)
gghistostats(
data = exam,
x = ENGLISH,
type = "bayes",
test.value = 60,
xlab = "English scores"
)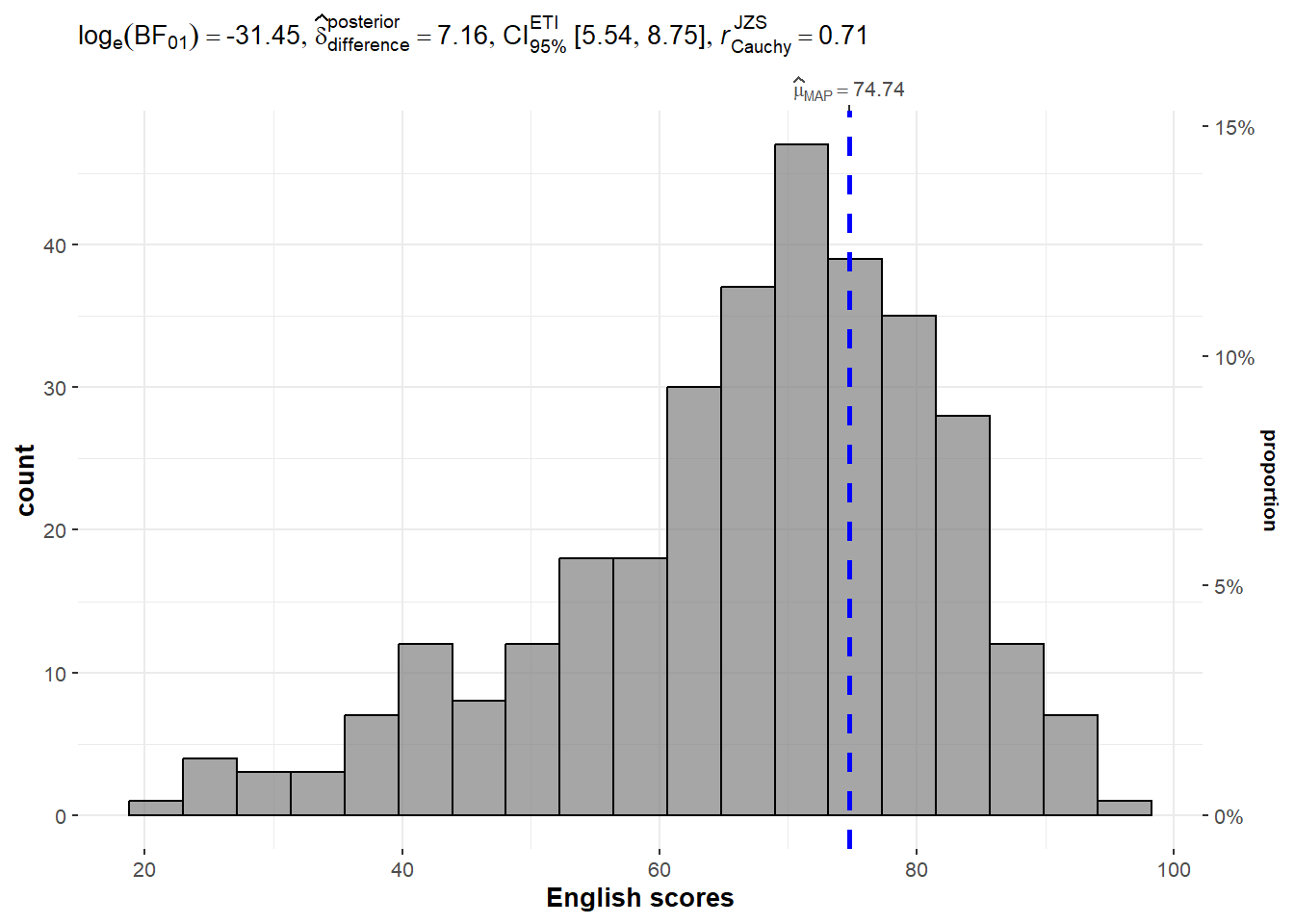
Unpacking the Bayes Factor
A Bayes factor is the ratio of the likelihood of one particular hypothesis to the likelihood of another. It can be interpreted as a measure of the strength of evidence in favor of one theory among two competing theories.
That’s because the Bayes factor gives us a way to evaluate the data in favor of a null hypothesis, and to use external information to do so. It tells us what the weight of the evidence is in favor of a given hypothesis.
When we are comparing two hypotheses, H1 (the alternate hypothesis) and H0 (the null hypothesis), the Bayes Factor is often written as B10. Null Hypothesis (H0): The true mean of the science scores is equal to the test value of 60. Alternative Hypothesis (H1): The true mean of the science scores is not equal to 60.
k log(n)- 2log(L(θ̂)): L(θ̂) represents the likelihood of the model tested, given your data, when evaluated at maximum likelihood values of θ.
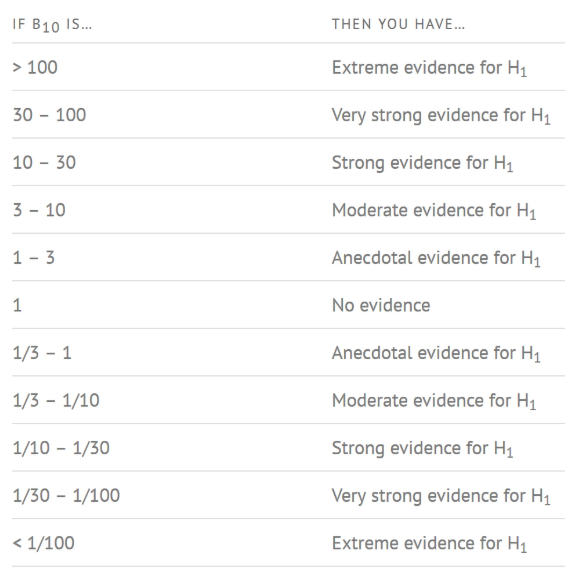
How to interpret Bayes Factor
A Bayes Factor can be any positive number. One of the most common interpretations is this one—first proposed by Harold Jeffereys (1961) and slightly modified by Lee and Wagenmakers in 2013:
Statistical Annotations:
- log_e(BF_01) = 2.12: This is the natural logarithm of the Bayes Factor (BF) comparing the null hypothesis (science scores = 60) to the alternative hypothesis. A Bayes Factor greater than 1 indicates evidence against the null, and the value here suggests that the data provide evidence against the null hypothesis H0 (since log_e(2.12) > 0).
- Δ_posterior mean = 1.12: This indicates the difference between the sample mean and the test value (60), suggesting the average score is higher than the test value.
- 95% CI: This confidence interval shows the range of values within which the true mean score lies with 95% probability, according to the posterior distribution.
- JZS = 0.71: This likely refers to the magnitude of the difference between groups or conditions.
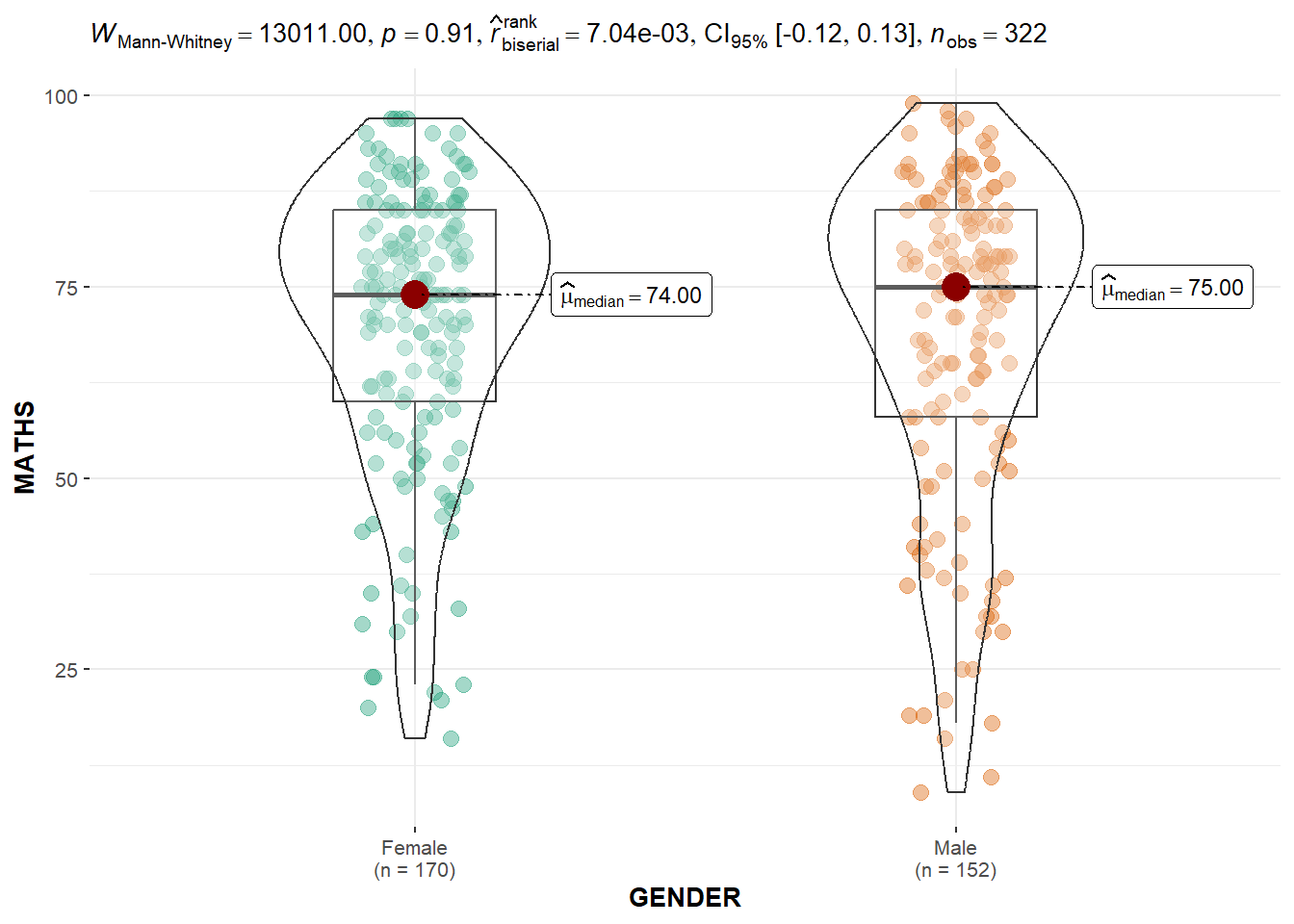
Two-sample mean test: ggbetweenstats()
In the code chunk below, ggbetweenstats() is used to build a visual for two-sample mean test of Maths scores by gender.
ggbetweenstats(
data = exam,
x = GENDER,
y = MATHS,
type = "np",
messages = FALSE
)
Oneway ANOVA Test: ggbetweenstats() method
In the code chunk below, ggbetweenstats is used to build a visual for One-way ANOVA test on English score by race.
ggbetweenstats(
data = exam,
x = RACE,
y = ENGLISH,
type = "p",
mean.ci = TRUE,
pairwise.comparisons = TRUE,
pairwise.display = "s",
p.adjust.method = "fdr",
messages = FALSE
)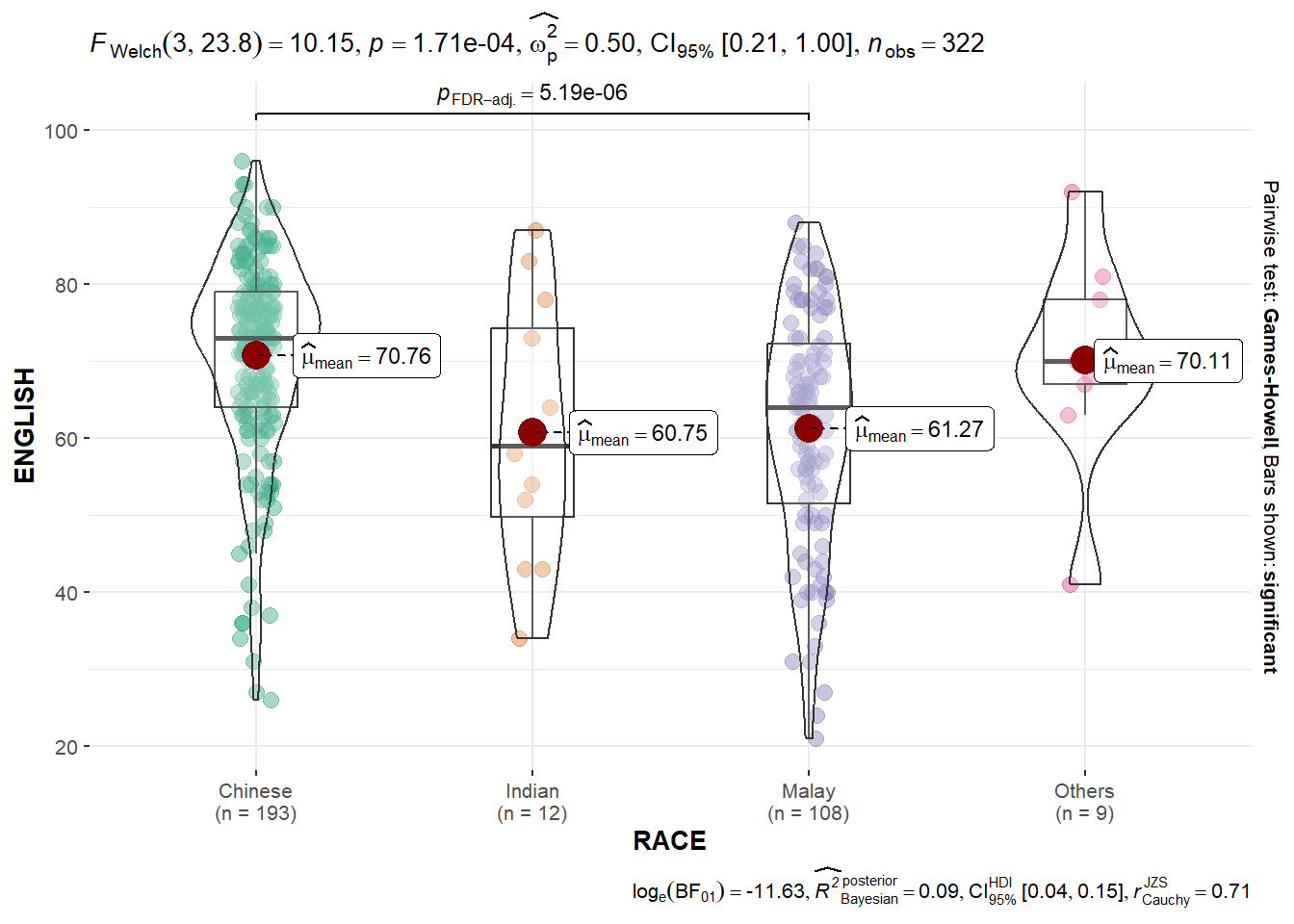
- “ns” → only non-significant
- “s” → only significant
- “all” → everything
ggbetweenstats - Summary of tests

 ## Significant Test of Correlation: ggscatterstats()
## Significant Test of Correlation: ggscatterstats()
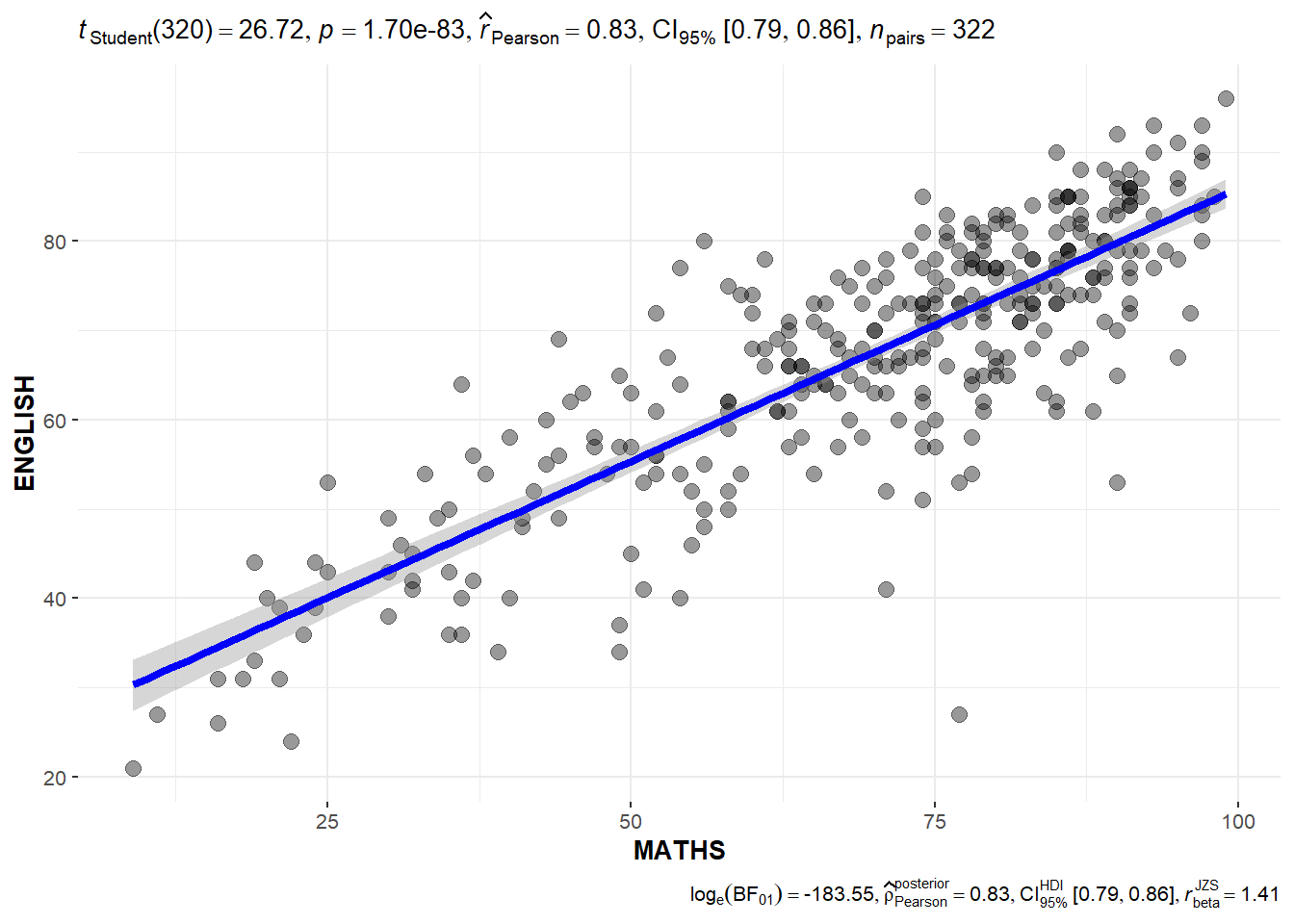
In the code chunk below, ggscatterstats() is used to build a visual for Significant Test of Correlation between Maths scores and English scores.
ggscatterstats(
data = exam,
x = MATHS,
y = ENGLISH,
marginal = FALSE,
)
Significant Test of Association (Depedence) : ggbarstats() methods
In the code chunk below, the Maths scores is binned into a 4-class variable by using cut().
exam1 <- exam %>%
mutate(MATHS_bins =
cut(MATHS,
breaks = c(0,60,75,85,100))
)In this code chunk below ggbarstats is used to build a visual for Significant Test of Association
ggbarstats(exam1,
x = MATHS_bins,
y = GENDER)